Refocusing
In paraxial optics, a well focused conventional camera is seen to project a far distant object point onto the image plane in a way that its image point is sharply focused and infinitesimally small. Given the same focus setting, another projected point from a much closer object would focus behind the sensor meaning that its directional rays are distributed over a larger portion of the image plane causing a blurred spot to occur on the output image. With traditional imaging, it is difficult to resolve blurred image areas. The plenoptic camera overcomes this limitation by the aid of a micro lens array and an image processing technique which is indicated below.
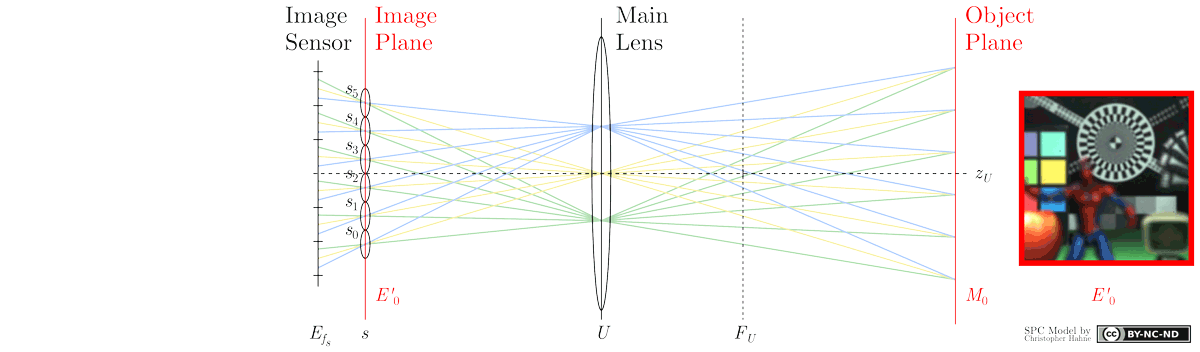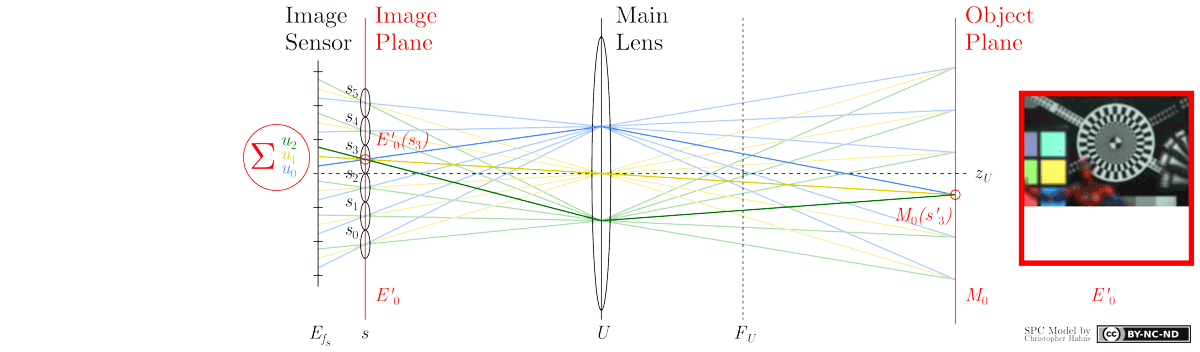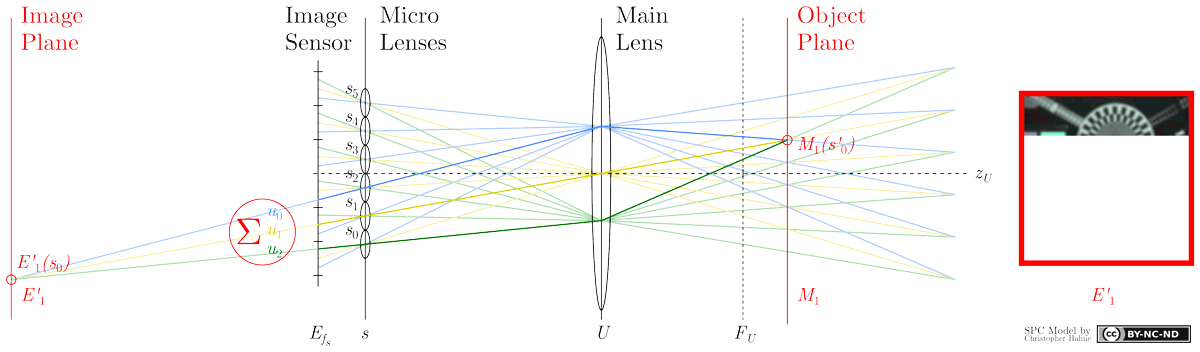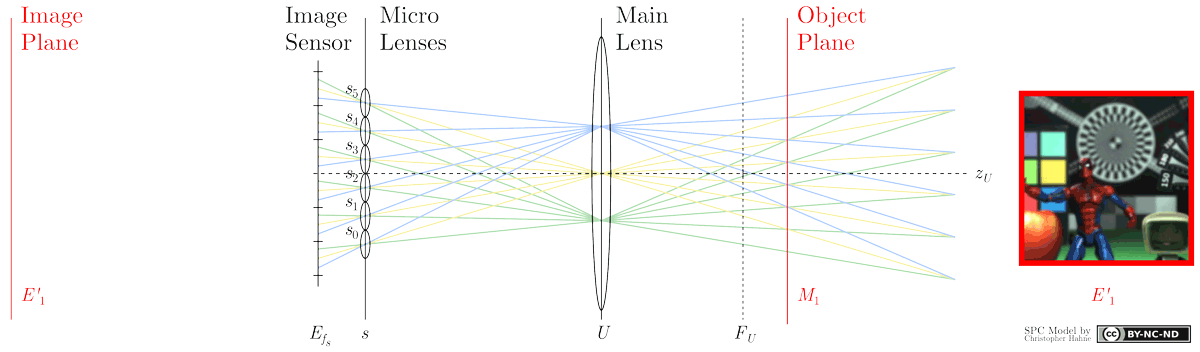
As highlighted in the animation, the light intensity of an image point E'0(s0) emitted from M0 is distributed over image sensor locations Efs(u0, s0), Efs(u1, s0) and Efs(u2, s0). Hence, by summing up these Efs values, the intensity at point E'0(s0) is retrieved. Upon closer inspection, it may be apparent that each image point at plane E'0 is obtained by calculating the sum of all pixel values within the respective micro image s.
As suggested by the term refocusing, another object plane, e.g. M1, may be computationally brought into focus from the same raw image capture. For instance, light rays emanating from a plane M1 can be thought of as projecting corresponding image points at E'1 behind the image sensor. The intensity of E'1(s0) is then recovered by integrating Efs intensities at positions (u2, s0), (u1, s1) and (u0, s2). From this example, it is seen that pixels selected to form image points behind the sensor are distributed over several micro images. In general, it can be stated that the closer the refocusable object plane Ma to the camera, the larger the gap between micro lenses from which pixels have to be merged. Recalling the second figure shown in the Sub-aperture section, an analogue representation is depicted below showing an approach to accomplish refocusing from previously extracted sub-aperture images.

While investigating the image refocusing process, the question came up what the distance to a refocused object plane Ma and its depth of field might be. A generic solution to this is discussed in the following.
Refocusing Distance and Depth of Field
According to the section Refocusing, it is possible to trace chief rays back to object space planes where they have been emitted from. Given all lens parameters of the Standard Plenoptic Camera, the slope of each chief ray within the camera as well as in object space may be retrieved and described as a linear function in a certain interval (e.g. from sensor image plane to micro lens). To approximate the metric distance of a refocusing plane Ma, the system of two arbitrary chief ray functions intersecting at plane Ma is solved.
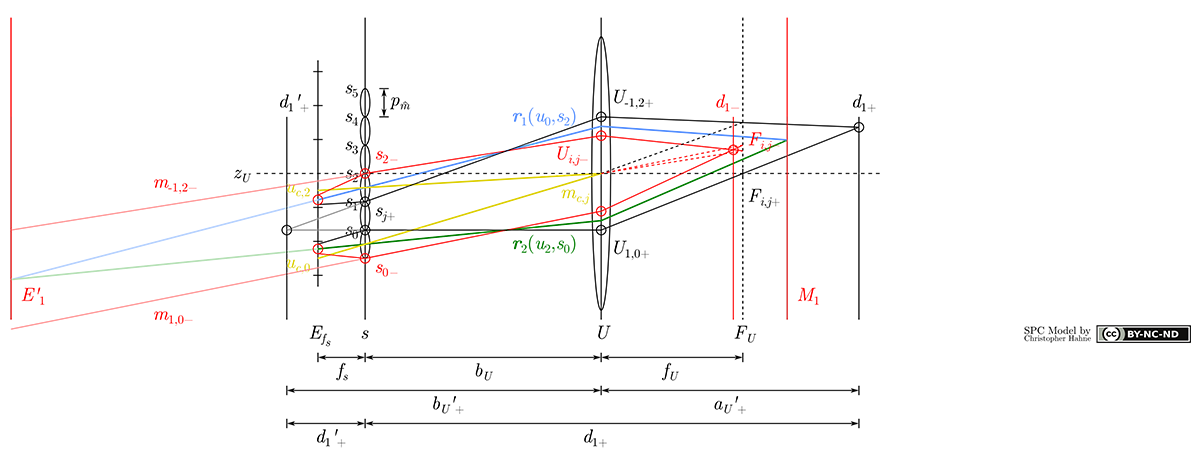
Based on the propositions made in section Model, a point u at the image sensor plane is seen to be of an infinitesimal size. However, lenses are known to diffract light and project a shape of an Airy pattern onto the image plane. Therefore, the width of u, which is due to lens diffraction, needs to be taken into consideration. Besides, sensor picture cells also have a finite size which is assumed to be greater than, or at least equal to, the lens diffraction pattern.
Tracing rays from sensor pixel boundaries in the same manner as described in section Model yields intersections in object space, denoted as da- and da+, in front of and behind the refocusing slice Ma, respectively. These planes indicate the depth of field of a single refocusing slice Ma. Object surfaces located within that depth range are 'in focus' meaning that objects located in that distance interval exhibit least blur. Mathematical derivation and validation results for the distance and depth estimation are found in the publications listed below.
Plenoptisign - Refocusing Distance Estimation
This section features a program to compute aforementioned light field parameters posed by any Standard Plenoptic Camera. It is its purpose to evaluate the impact of optical parameters on the depth resolution capabilities of your plenoptic camera. This may be useful (but not limited to) an early design phase, prototyping stage or calibration-free conceptualisation of a plenoptic camera that requires metric precision outputs.
Feel free to play with the default values and press "Run" to obtain your estimation results.
Demo (runs cgi_script.py)
Source Code
Related Publications
PlenoptiCam v1.0: a light-field imaging framework
C. Hahne and A. Aggoun "PlenoptiCam: a light-field imaging framework," IEEE Transactions on Image Processing, vol. 30, pp. 6757-6771 (2021).
PlenoptiSign: an optical design tool for plenoptic imaging
C. Hahne and A. Aggoun "PlenoptiSign: an optical design tool for plenoptic imaging," Software X, vol. 10 (2019).
Refocusing distance of a standard plenoptic camera
C. Hahne, A. Aggoun, and V. Velisavljevic, S. Fiebig, and M. Pesch "Refocusing distance of a standard plenoptic camera," Opt. Express 24, Issue 19, pp. 21521-21540 (2016).
[PDF] [BibTeX] [Code] [Zemax file] [Image data]
The standard plenoptic camera: applications of a geometrical light field model
C. Hahne, "The standard plenoptic camera: applications of a geometrical light field model," PhD thesis, Univ. of Bedfordshire, (January, 2016).
If you have any questions, feel free to contact me via info [ät] christopherhahne.de